Game theory is a branch of applied mathematics that uses models to study interactions with formalised incentive structures ("games"). Unlike decision theory, which also studies formalized incentive structures, game theory encompasses decisions that are made in an environment where various players interact strategically. In other words, game theory studies choice of optimal behavior when costs and benefits of each option are not fixed, but depend upon the future choices of other individuals. It has applications in a variety of fields, including economics, international relations, evolutionary biology, political science, and military strategy. Game theorists study the predicted and actual behaviour of individuals in games, as well as optimal strategies. Seemingly different types of interactions can exhibit similar incentive structures, thus all exemplifying one particular game.
John von Neumann and Oskar Morgenstern first formalised the subject in 1944 in their book Theory of Games and Economic Behavior. Game theory has important applications in fields like operations research, economics, collective action, political science, psychology, and biology. It has close links with economics in that it seeks to find rational strategies in situations where the outcome depends not only on one's own strategy and "market conditions", but upon the strategies chosen by other players with possibly different or overlapping goals. Applications in military strategy drove some of the early development of game theory.
Game theory has come to play an increasingly important role in logic and in computer science. Several logical theories have a basis in game semantics. And computer scientists have used games to model interactive computations. Computability logic attempts to develop a comprehensive formal theory (logic) of interactive computational tasks and resources, formalising these entities as games between a computing agent and its environment.
Game theoretic analysis can apply to simple games of entertainment or to more significant aspects of life and society. The prisoner's dilemma, as popularized by mathematician Albert W. Tucker, furnishes an example of the application of game theory to real life; it has many implications for the nature of human co-operation, and has even been used as the basis of a game show called Friend or Foe?.
Biologists have used game theory to understand and predict certain outcomes of evolution, such as the concept of evolutionarily stable strategy introduced by John Maynard Smith and George R. Price in a 1973 paper in Nature (See also Maynard Smith 1982). See also evolutionary game theory and behavioral ecology. Analysts of games commonly use other branches of mathematics, in particular probability, statistics and linear programming, in conjunction with game theory.
Mathematical definitions:
There are a few alternative definitions of the notion of a 'game'.
Normal form game design:
A game in normal or strategic form combines the set of possible
strategies for each player and records the payoffs for each outcome.
Let N be a set of players. For each player there is given a set
of strategies![]() . The game is then a function:
. The game is then a function:

So that, if one knows the tuple of strategies that were chosen by the players, one is given the allocation payments, a real number assignment. A further generalization can be achieved by splitting the game into two functions: the normal form game, describing the way in which strategies define outcomes, and a second function depicting player's preferences on the set of outcomes. Hence:
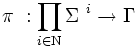
Where is the outcome set of the game. And for each player there is a preference function.
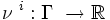
A reduced normal form exists as well. The reduced normal form combines strategies for which are associated with the same payoffs.
Read more...